树
# 树的概念
树是一种非线性的数据结构,用它能很好地描述有分支和层次的数据集合。
一棵树由n(n>=0)个节点组成的有限集合以及该集合上定义的一种节点关系。
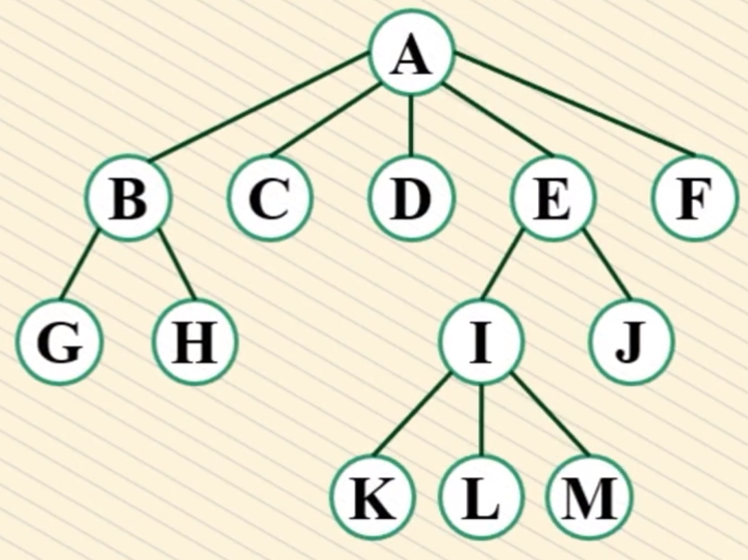
树的节点:集合中每个元素称为树的节点。
根节点(树根):一棵树只有一个根节点,位于最顶层(第一层)
子树:除根节点外,其余节点能分成m(m>=0)个互不相交的有限集合。这些子集称为这棵树的子树。树是递归定义的。
节点的度:节点的子树数目。
树的度:树中各节点的度的最大值。
树的广度(宽度):节点的度和树的度共同体现了树的宽度。
树的深度(高度):树的层次,有几层就有多高。根节点的层次为1.
内部节点:根以外的分支节点。
叶节点(终端节点):度为0的节点。
分支节点(非终端节点):度非0的节点。
父节点、子节点(孩子节点)、兄弟节点、祖先节点、子孙节点
前驱:根节点没有前驱,除根节点外,其余节点有唯一的前驱。
后继:叶节点没有后继,除叶节点外,其余节点有一个或多个后继。
边(树枝):连接两个节点的线段。n个节点有n-1条边。
路径:任意两个不同的节点,如果从一个节点出发,自上而下沿树枝能到达另一节点,称它们之间存在一条路径。路径的长度等于路径上节点个数减1。
# 树的分类
根据树节点的有序性,可以将树结构分为两类:查找树和无序树。
根据树分支的数量限制,可以将树结构分为两类:多叉树和二叉树。
# 查找树
查找树:也可以叫搜索树,任意一个节点所包含的键值,大于等于左孩子的键值,小于等于右孩子的键值。
# 无序树
无序树:节点的键值无特定大小关系。
# 多叉树
在多叉树上每一个节点可以有两个或两个以上的子节点。
# 二叉树
二叉树(binary tree,BT),是一种特殊的树型结构。它的度数为2,即每个节点最多有两个子节点。
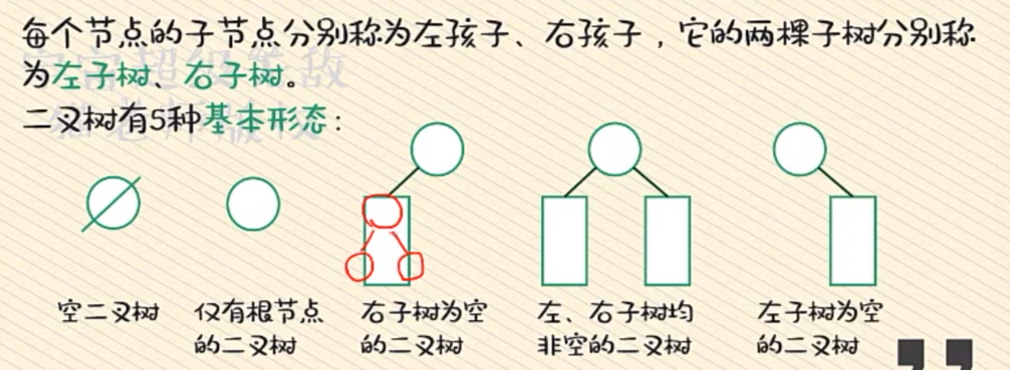
# 二叉树的性质
在二叉树的第 i 层最多有 2的i减1次方 个节点。
深度为 k 的二叉树至多有 2的k次方减1 个节点。
# 二叉树的遍历
- 先序遍历:中左右,根节点->左子树->右子树。
- 中序遍历:左中右,左子树->根节点->右子树。
- 后序遍历:左右中,左子树->右子树->根节点。
- 层级遍历:先上后下,先左后右。
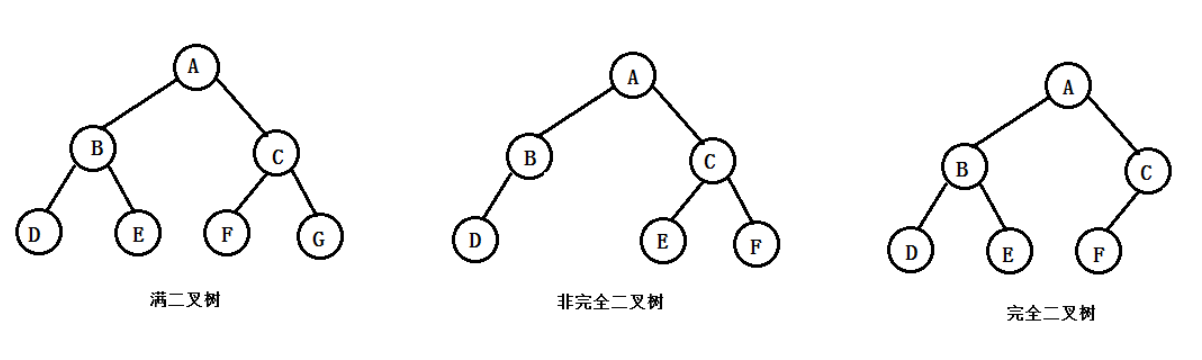
# 满二叉树和完全二叉树
满二叉树:深度为 k 且有 2的k次方减1 个节点的树。除叶节点外的所有节点均有两个子节点。节点数达到最大值。所有叶节点必须在同一层上。
完全二叉树:深度为k,除第k层外,其它各层(1~k-1)的节点数都达到最大值,第k层所有节点连续集中在最左边。除最后一层外,每一层上的节点数均达到最大值;在最后一层上只缺少右边的若干节点。
# AVL Tree
AVL树,自平衡二叉查找树,有以下特点:
- 左子树和右子树都是AVL树
- 左子树和右子树的高度差不能超过 1
- 增加和删除节点可能需要通过多次旋转操作使树结构达到平衡,故增删效率较低,但平衡后降低树了的高度,故搜索效率较高。
# R-B Tree
红黑树(Red-Black Tree,简称R-B Tree),是一种特殊的二叉查找树,是相对接近平衡的二叉树,它只要求部分平衡,任何不平衡都会在三次旋转之内解决,故其增删效率相对 AVL 树更高,查询效率则稍逊。
红黑树的每个节点上都有存储位表示节点的颜色,颜色是红(Red)或黑(Black),其特性如下:
- 节点非黑即红
- 根节点为黑色
- 叶节点为黑色(叶节点是指末梢的空节点
Nil或Null) - 一个节点为红色,则其两个子节点必须是黑色的(根到叶子的所有路径,不可能存在两个连续的红色节点)
- 每个节点到叶子节点的所有路径,都包含相同数目的黑色节点(相同的黑色高度、黑色完美平衡)
红黑树通过变色、左旋和右旋实现黑色完美平衡。
- 变色:红色变黑色、黑色变红色
- 左旋:父节点成为右儿子的左子树,右儿子原本的左子树成为父节点的右子树。
- 右旋:父节点成为左儿子的右子树,左儿子原本的右子树成为父节点的左子树。
在插入节点时,首先确定插入节点的位置,然后平衡插入,即通过变色、左旋、右旋实现根节点到所有叶节点路径上黑色完美平衡。
如果插入节点的父节点为黑色,直接插入即可。
如果插入节点的父节点为红色,需要平衡插入。
# 森林
森林是m(m>=0)棵互不相交的树的集合。
# 相关链接
Data Structure Visualizations - 数据结构可视化网站 (opens new window)
数据结构-二叉树(上) (opens new window)
